Bringing Physics into Generative Models: Bridging SPDE and Gradient flow Models

Neural Variational Data Assimilation with Uncertainty Quantification Using SPDE Priors

Paper published at Artificial Intelligence for the Earth Systems - American Meteorological Society

Overview

Large-scale geophysical datasets from satellites and numerical simulations have traditionally been analyzed using Optimal Interpolation (OI) or model-based data assimilation. While effective, these classical methods face computational challenges with high-dimensional data due to dense covariance matrices. Meanwhile, deep learning approaches have emerged as powerful alternatives, but they often lack robust uncertainty quantification and physical interpretability.

In our recent work, we bridge these two paradigms by combining Stochastic Partial Differential Equations (SPDEs) with neural architectures to create a framework that:

Captures non-stationary spatial and temporal covariances
Learns both system states and SPDE parameters jointly
Provides principled uncertainty quantification
Enables real-time data assimilation and short-term forecasting

The Challenge: High-Dimensional Spatio-Temporal Reconstruction

Consider reconstructing ocean surface height from sparse satellite observations covering less than 10% of the domain at any given time. Traditional Optimal Interpolation solves:

\[\mathbf{x}^\star = \arg \min_\mathbf{x} \|\mathbf{y}-\mathbf{H}_\Omega \mathbf{x}\|^2_\mathbf{R} + \lambda \|\mathbf{x}-\mu\|^2_\mathbf{P}\]

where $\mathbf{y}$ represents noisy observations, $\mathbf{H}_\Omega$ is the observation operator, and $\mathbf{P}$ is the prior covariance. However, for high-dimensional problems with thousands of grid points over multiple time steps, computing and inverting $\mathbf{P}$ becomes intractable.

Our Approach: SPDE-Based Gaussian Processes

We leverage the elegant connection between SPDEs and Gaussian Processes (GPs) discovered by Lindgren et al. (2011). A continuous spatio-temporal process can be described by:

\[d\mathbf{x} = \mathcal{F}(\mathbf{x}, t)\, dt + \mathcal{G}(\mathbf{x}, t)\, d\mathbf{w}\]

where $\mathcal{F}$ is the drift operator capturing advection and diffusion dynamics, and $\mathcal{G}$ controls the stochastic forcing. Through backward Euler discretization, this yields a discrete state-space model:

\[\mathbf{x}_{t+1} = \mathbf{M}_{t+1}\, \mathbf{x}_t + \boldsymbol{z}_{t+1}, \quad \boldsymbol{z}_{t+1} \sim \mathcal{N}(0, \mathbf{Q}_{z,t+1}^{-1})\]

The key insight is that the SPDE formulation produces sparse precision matrices $\mathbf{Q}$, enabling efficient computation even for large-scale problems. The differential operator takes the form:

\[\mathbf{F} = \left(\boldsymbol{\kappa}^2_t - \nabla \!\cdot\! \mathbf{m}_t - \nabla \!\cdot\! \mathbf{H}_t \nabla \right)^{\!\alpha/2}\]

where:

$\mathbf{m}_t$: advection vector (captures flow direction)
$\mathbf{H}_t$: diffusion tensor (captures anisotropic smoothing)
$\boldsymbol{\kappa}_t$: spatial scaling factor
$\alpha$: smoothness parameter of the underlying GP

Neural SPDE Solver Architecture

Rather than manually tuning SPDE parameters or solving expensive optimization problems at inference time, we propose a neural variational solver that learns to:

Iteratively refine the state using a gradient-based update: $\mathbf{x}^{(k+1)} = \mathbf{x}^{(k)} - \mathcal{K}\!\left[\nabla_\mathbf{x} \mathcal{J}_\Phi(\mathbf{x}^{(k)},\mathbf{y},\Omega)\right]$ where $\mathcal{K}$ is a neural operator (ConvLSTM + linear layer)
Jointly optimize state and SPDE parameters through a bi-level loss: $\min_{\Gamma,\boldsymbol{\Theta}} \lambda_1 \|\mathbf{x}-\mathbf{x}^\star\|^2 + \lambda_2 \big[-\log p(\mathbf{x}\mid\boldsymbol{\Theta}^\star)\big]$

The augmented state $\tilde{\mathbf{x}}=[\mathbf{x},\boldsymbol{\Theta}]^\top$ includes both the physical field and the SPDE parameters $\boldsymbol{\Theta}={\boldsymbol{\kappa},\mathbf{m},\mathbf{H},\boldsymbol{\tau}}$.

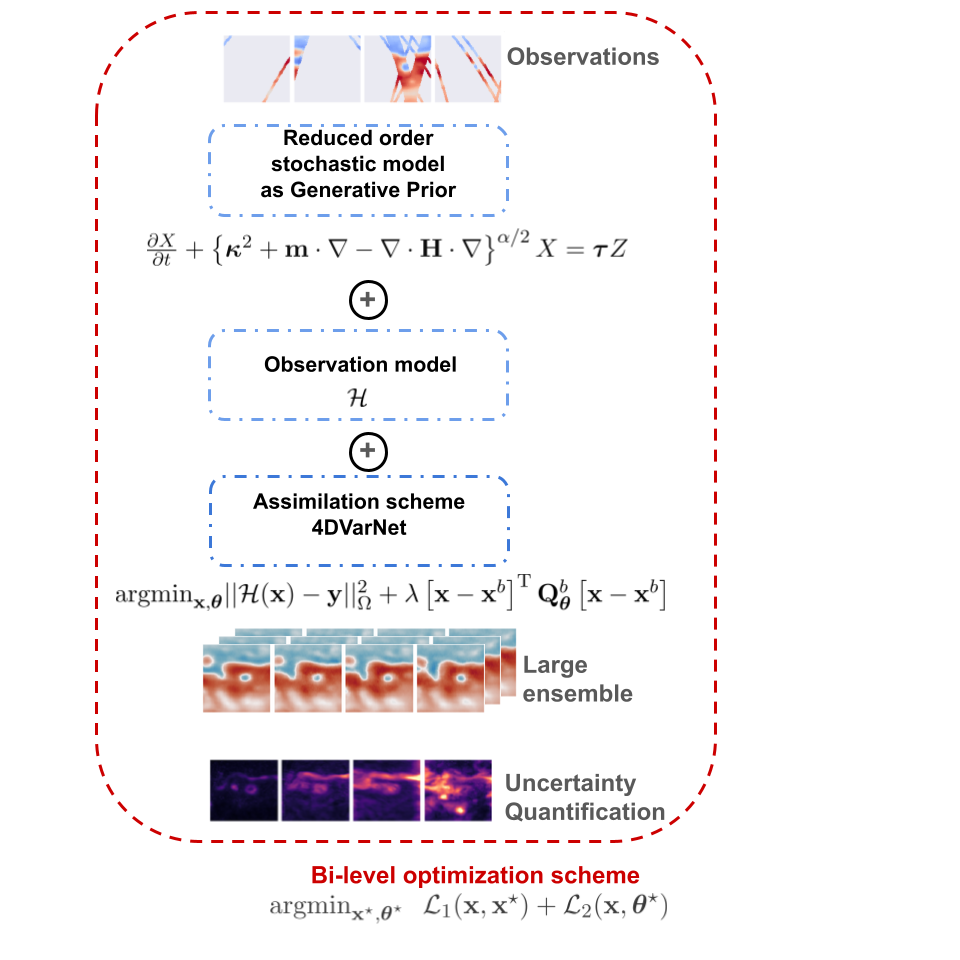Neural SPDE Architecture Concept Conceptual overview: The neural solver iteratively refines the state while learning interpretable SPDE parameters

Uncertainty Quantification Through Conditional Sampling

A major advantage of our approach is principled uncertainty quantification. By sampling from the SPDE prior and conditioning on observations, we generate ensemble members following:

\[\mathbf{x}^{\star,i} = \mathbf{x}^\star + (\mathbf{x}_s^i - \mathbf{x}_s^{\star,i})\]

where $\mathbf{x}_s^i$ is a stochastic SPDE simulation and $\mathbf{x}_s^{\star,i}$ its reconstruction. This kriging-based approach provides physically consistent posterior samples without expensive MCMC.

Experimental Results: Ocean Altimetry

We evaluate our framework on the OceanBench SSH mapping challenge using the NATL60 simulation over the Gulf Stream region (10°×10° domain, 1/20° resolution, >90% missing data).

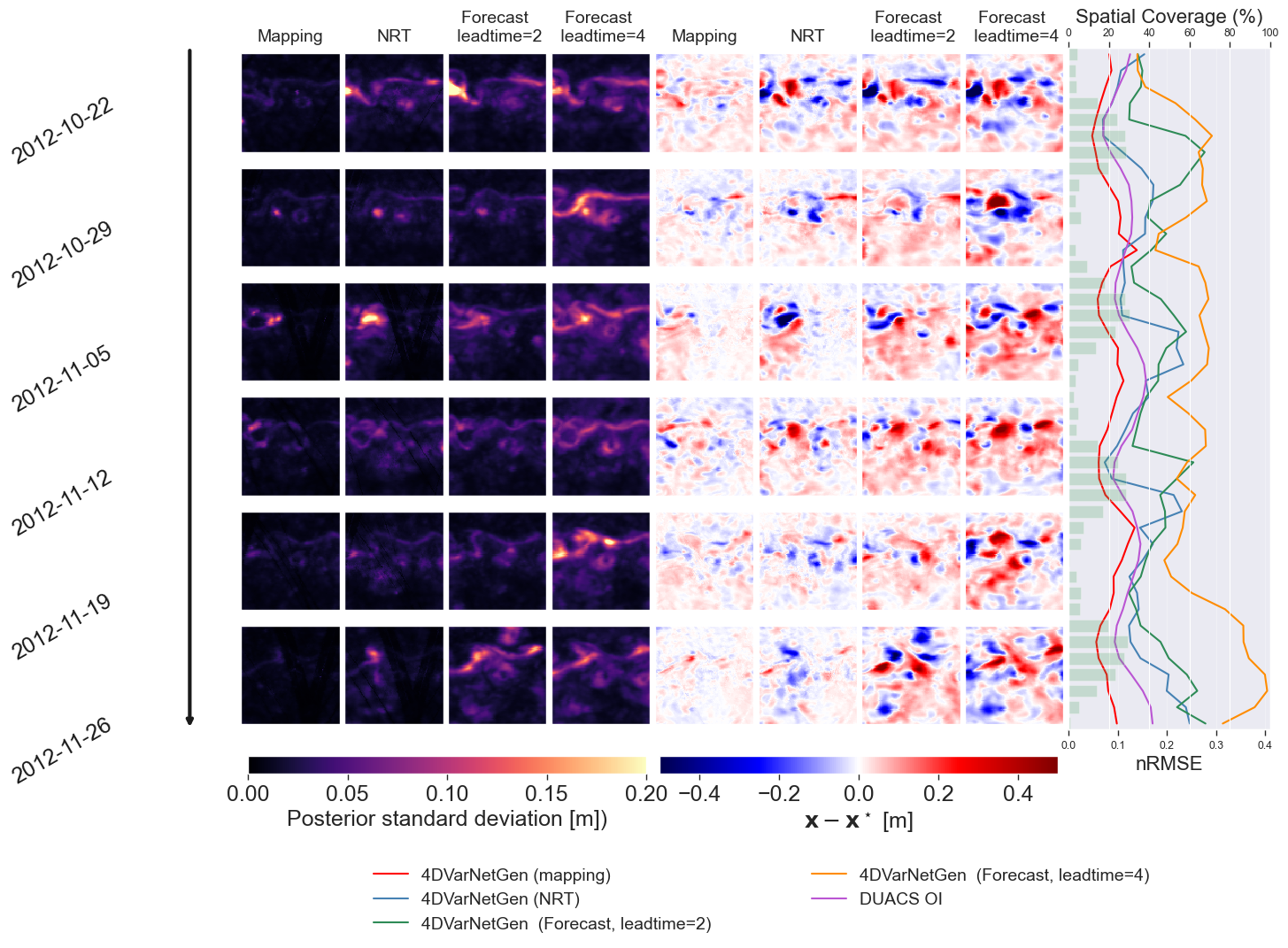Reconstruction and Uncertainty From left to right: [columns 1-4] Ensemble-based posterior standard deviations for mapping, near-real-time (NRT) and short-term forecast with lead times 2 and 4 (FOR2 and FOR4) for 6 days evenly spaced of 7 days along the test period; [columns 5-8] reconstruction error for mapping, NRT, FOR2 and FOR4 for the same 6 days evenly spaced of 7 days along the test period; normalized RMSE over the entire test period for mapping, NRT, FOR2 and FOR4 together with the daily spatial coverage of the SST pseudo-observations given as complementary green bar plots scaled on the right-hand side of the time series.

Key Performance Metrics

Method	RMSE	σ(RMSE)	λₓ (deg)	λₜ (days)
DUACS OI (mapping)	0.92	0.02	1.22	11.06
4DVarNet-Gen (mapping)	0.94	0.01	0.86	8.71
4DVarNet-Gen (NRT)	0.89	0.03	1.22	9.9
4DVarNet-Gen (FOR2)	0.88	0.03	1.20	13.74
4DVarNet-Gen (FOR4)	0.81	0.04	1.37	22.92

Our method achieves:

50% RMSE reduction vs. operational DUACS baseline
20-25% improvement vs. MIOST and UNet baselines
Successfully resolves temporal scales below 10 days
Provides flow-dependent uncertainty that matches reconstruction error patterns

Interpretable SPDE Parameters

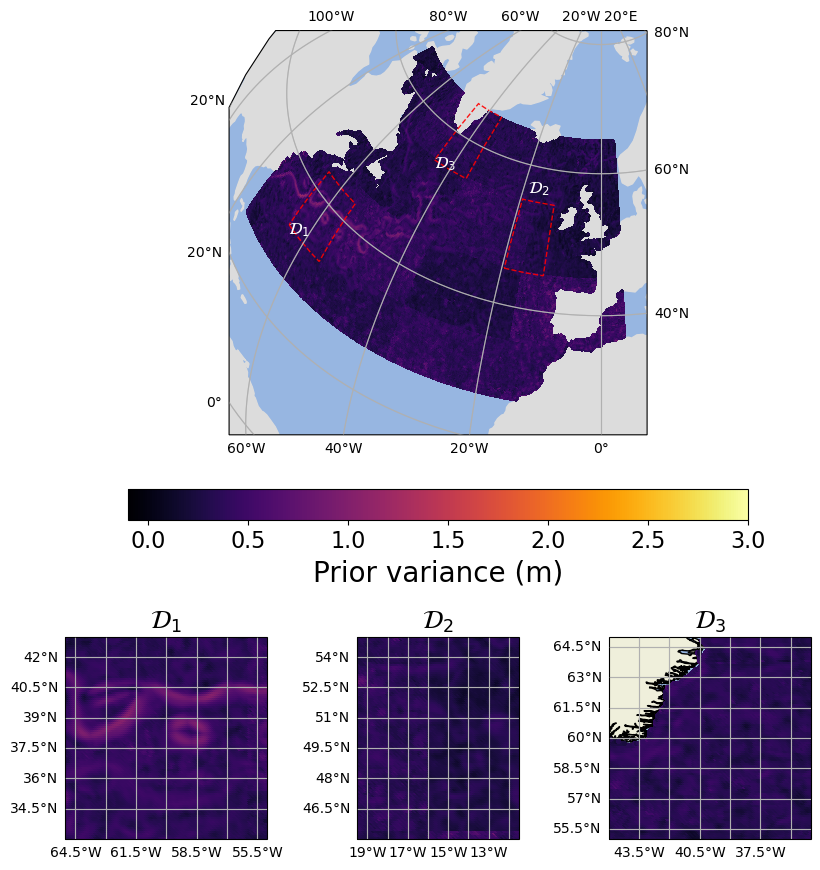
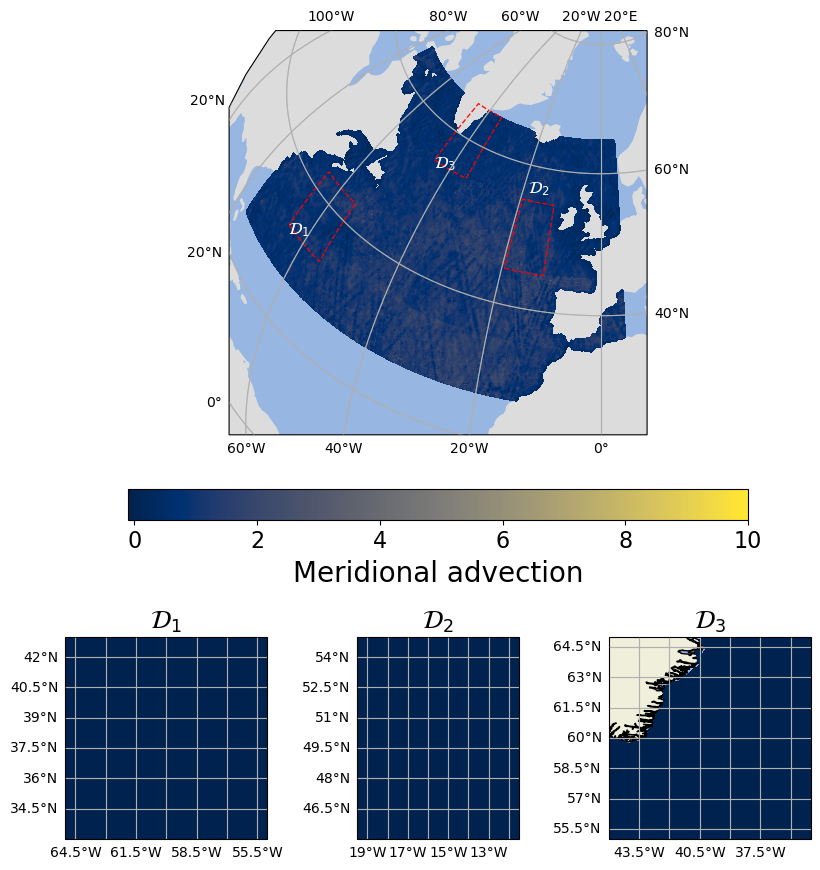
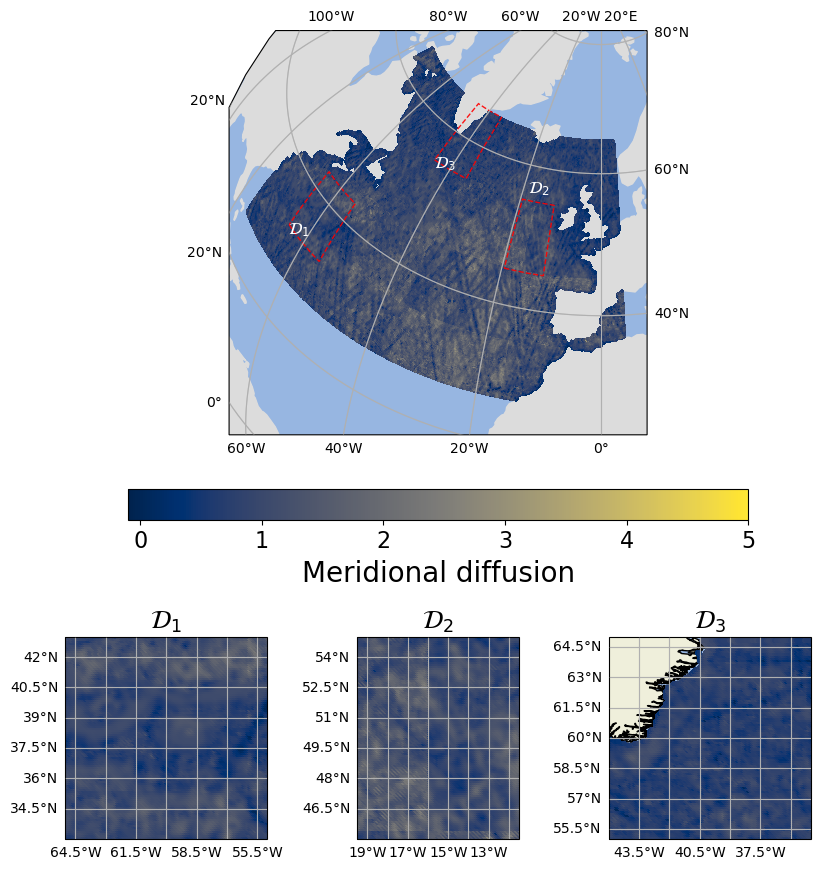Learned SPDE parameters over the North Atlantic: (a) local variance τ, (b) meridional advection m₁, (c) meridional diffusion H₁₁. The model automatically identifies regions of high variability (Gulf Stream meanders), dominant flow directions, and anisotropic smoothing patterns.

The learned parameters reveal physically meaningful patterns:

Higher variance along energetic regions (Gulf Stream, eddies)
Advection vectors aligned with ocean currents
Anisotropic diffusion following flow topology

Forecasting Capabilities

By masking future time steps during training, the model learns to forecast from past observations. The framework maintains stable performance even for 4-day lead times:

FOR2 (2-day forecast): 0.88 normalized RMSE, retains mesoscale structures
FOR4 (4-day forecast): 0. 81 normalized RMSE, controlled error growth
Uncertainty properly increases with forecast horizon

The right panel in the first figure shows how RMSE remains stable for mapping and NRT, then rises smoothly for forecasts, indicating well-calibrated confidence.

Connections to Generative Models

Our framework shares deep connections with modern generative models:

Score-based models: The gradient of our variational cost resembles score matching: $\nabla_{\mathbf{x}} \mathcal{J}(\mathbf{x},\mathbf{y},\Omega) = \nabla_{\mathbf{x}} \log p(\mathbf{y}|\mathbf{x}) + \nabla_{\mathbf{x}} \log p(\mathbf{x})$

Diffusion models: The SPDE evolution can be viewed as a reverse diffusion process: $\mathbf{x}_{t+1} = \mathbf{x}_t - \mathbf{F}_{t+1}\mathbf{M}_{t+1} \mathbf{x}_t + \mathbf{T}_{t+1}\boldsymbol{z}_{t}$

VAE formulation: The SPDE acts as a structured decoder, while the neural solver learns to infer latent SPDE parameters (encoder).

These connections position our work at the intersection of physics-based modeling and deep generative frameworks, offering a path toward interpretable, physics-aware generative models for scientific applications.

Transfer Learning to Global Scale

The framework demonstrates strong transfer learning capabilities. Models trained on regional domains (Gulf Stream) successfully generalize to global-scale SSH reconstruction with minimal fine-tuning:

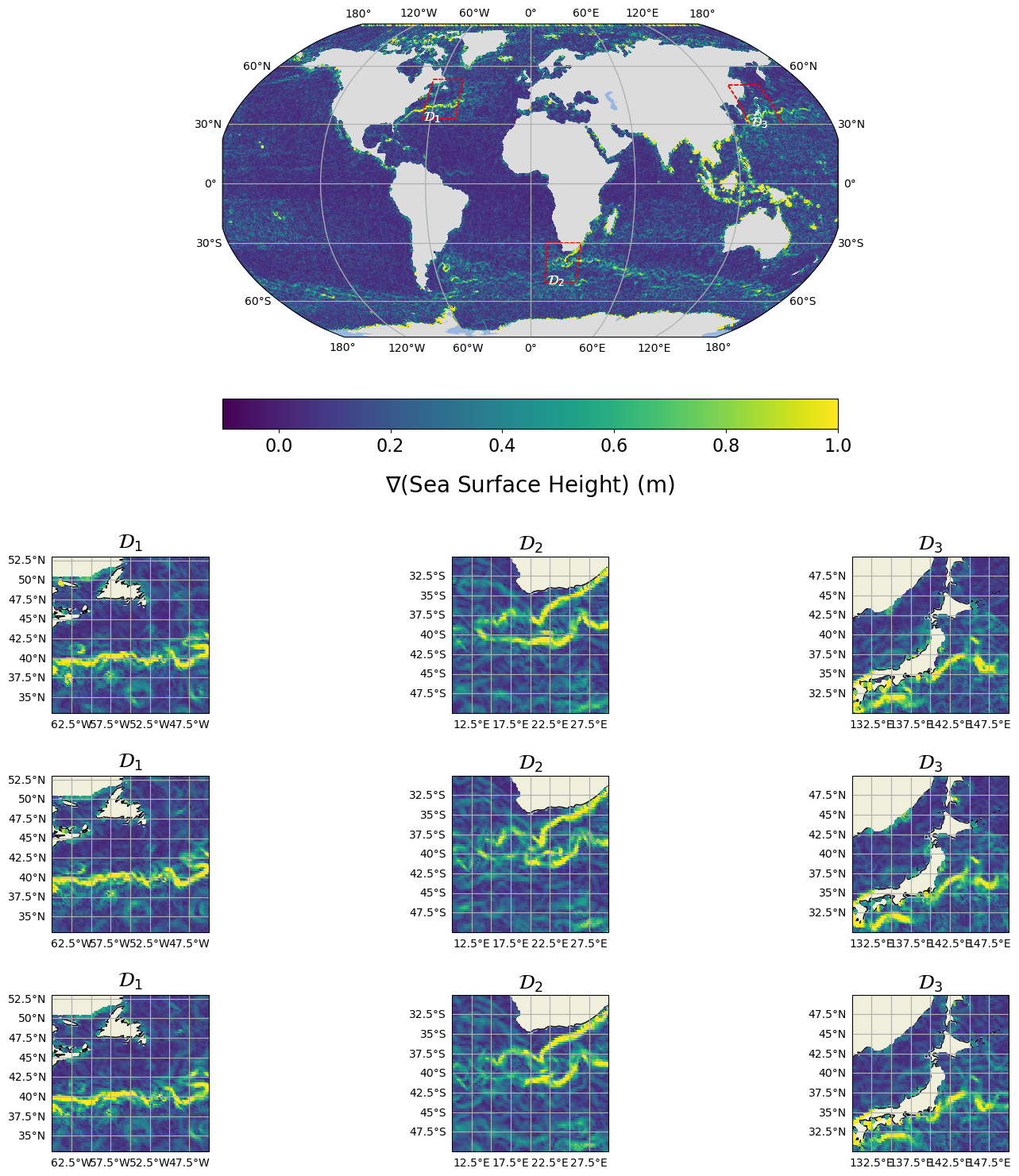Global Scale Transfer Ground truth and three posterior ensemble members for a 2-day forecast over the Global domain, with three subdomains highlighted (red boxes) corresponding to the Gulf Stream, Agulhas, and Kuroshio currents

Computational Efficiency

Training: ~10 hours on single NVIDIA A100 GPU (Gulf Stream domain)
Inference: Few seconds for full reconstruction
Global scale: <1 minute for transfer learning
Scalability: Sparse precision matrices enable $O(Nm^3)$ complexity vs. $O(N^3m^3)$ for dense methods

Key Takeaways

Unified framework: Combines interpretable SPDE priors with flexible neural solvers
Robust UQ: Provides flow-dependent uncertainty through conditional SPDE sampling
Forecasting: Naturally extends to short-term prediction (2-4 day horizons)
Scalability: Sparse precision matrices enable global-scale applications
Interpretability: Learned parameters reveal physical processes (advection, diffusion, variance)
Generative AI: Connects classical DA with modern diffusion/score-based models

Future Directions

Extension to nonlinear SPDEs for complex dynamics
Integration with physics-informed loss functions
Application to multi-variate systems (ocean temperature, salinity, currents)
Exploration of stochastic solvers via Langevin dynamics
Real-data validation beyond OSSE experiments

References

Full paper available at AIES American Meteorological Society

Code and implementation: GitHub Repository

Dataset: OceanBench SSH Mapping Challenge

This work represents a step toward physics-aware generative models that combine the interpretability of classical methods with the flexibility of deep learning, enabling robust data assimilation and forecasting for complex geophysical systems.

Maxime Beauchamp